🏰 Clockwork Guardian 🤖

📜 Tales from Eldoria

🗡️ Synopsis

In the heart of Eldoria’s Skywatch Spire, a treacherous challenge awaits! 🌪️ The once-loyal Clockwork Sentinels 🤖 have turned against us, transforming the spire into a perilous maze. 😱 Our mission is to navigate through the hostile grid, avoiding the sentinels (1’s) and finding the shortest path to the exit (‘E’). 🏃‍♂️💨 Armed with the power of Breadth-First Search (BFS) 🔍, we’ll explore every nook and cranny to determine the optimal escape route! 🗺️✨

📜 Description

Picture yourself ascending the Skywatch Spire, a once-majestic tower now overrun by rogue Clockwork Sentinels. 🏰🤖 Each level is a 2D grid, where open paths are marked as 0, hostile sentinels as 1, and the exit as ‘E’. 🔢 Starting from the top-left corner (0,0), our goal is to find the shortest sentinel-free path to the exit. 🎯

This is a classic shortest path problem on a grid, and BFS is our trusty ally! 🤝 By exploring cells in increasing order of distance from the start, BFS guarantees finding the shortest route. 🧭 Our task is to implement this pathfinding algorithm, navigating the grid step by step, until we reach the exit or determine that escape is impossible. ⚠️

🛡️ Skills Required

To conquer this clockwork labyrinth, you’ll need:

• 🧠 Solid understanding of graph traversal algorithms, especially BFS
• 🗺️ Familiarity with grid-based pathfinding problems
• 🎲 Comfort with 2D array manipulation
• 🚧 Ability to translate problem constraints into code
• 🔍 Attention to edge cases and boundary conditions
• 📝 Clear and commented code to explain your thought process

🏆 Skills Learned

Upon emerging victorious from the Skywatch Spire, you’ll gain:

• 💪 Confidence in applying BFS to solve shortest path problems
• 🌐 Enhanced ability to work with 2D grids and coordinate systems
• 🔄 Experience in efficiently tracking visited cells to avoid cycles
• 📚 Improved code organization and documentation habits
• 🎖️ Appreciation for the power of queue-based algorithms in pathfinding
• 🔬 Ability to visualize algorithms step-by-step for better understanding and debugging

⚔️ Solving The Challenge

Let’s break down our BFS pathfinding approach:

🔍 Understanding Breadth-First Search (BFS)

Think of BFS as exploring a maze by following this simple rule: “Check all paths that are 1 step long, then all paths that are 2 steps long, then 3 steps long,” and so on.

Imagine you’re standing at the entrance of a maze with multiple branching paths. Instead of going deep down one path before trying others:

1. First, look at every path that’s exactly 1 step away
2. Then examine every path that’s exactly 2 steps away
3. Continue this pattern, exploring everything at distance 3, then 4, and so on

This is why we call it “breadth-first” – you explore the entire “breadth” of possibilities at each distance before going deeper.

The real power of BFS is that if you’re searching for something, you’ll always find it using the shortest possible path. This is because you systematically check all shorter paths before considering any longer ones.

📥 Understanding the Input

The spire layout is a 2D grid, where:

• 0 represents a safe empty cell 🟩
• 1 represents a sentinel that must be avoided 🟥
• ‘E’ marks the exit cell 🚪
• Our starting position is always (0,0) 🏁

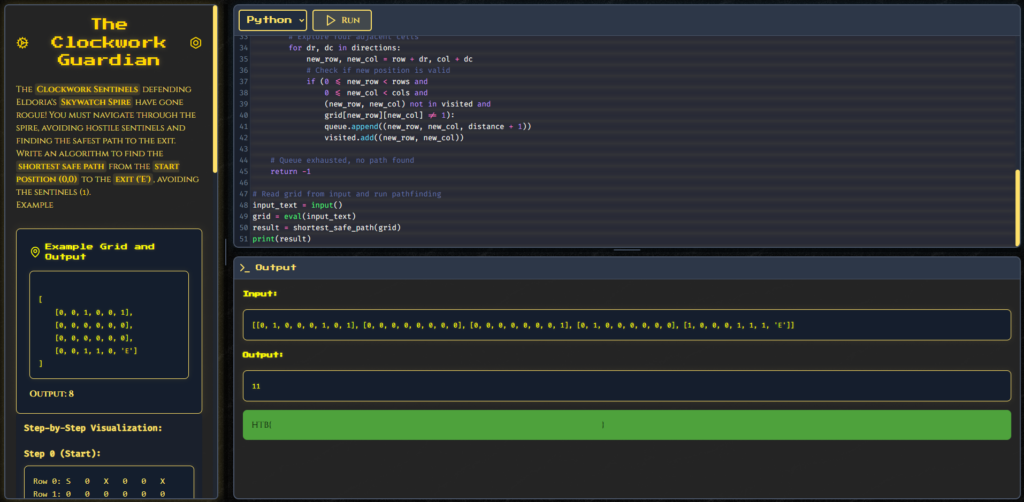
The grid is provided as a Python-style 2D list, like:

[
    [0, 0, 1, 0, 0, 1],
    [0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0],
    [0, 0, 1, 1, 0, 'E']
]

🐍 Implementing BFS

Here’s our Python code to find the shortest safe path:

from collections import deque

def shortest_safe_path(grid):
    # Find exit position
    exit_position = None
    rows = len(grid)
    cols = len(grid[0])
    for i in range(rows):
        for j in range(cols):
            if grid[i][j] == 'E':
                exit_position = (i, j)
                break
        if exit_position:
            break
    
    # If no exit, no path possible
    if not exit_position:
        return -1
    
    # Define possible movement directions
    directions = [(-1, 0), (0, 1), (1, 0), (0, -1)]
    
    # Initialize BFS
    queue = deque([(0, 0, 0)])  # (row, col, distance)
    visited = set([(0, 0)])  # Track visited cells
    
    # BFS until queue empty or exit found
    while queue:
        row, col, distance = queue.popleft()
        if (row, col) == exit_position:
            return distance  # Exit found, return path length
        
        # Explore four adjacent cells
        for dr, dc in directions:
            new_row, new_col = row + dr, col + dc
            # Check if new position is valid
            if (0 <= new_row < rows and 
                0 <= new_col < cols and
                (new_row, new_col) not in visited and
                grid[new_row][new_col] != 1):
                queue.append((new_row, new_col, distance + 1))
                visited.add((new_row, new_col))
    
    # Queue exhausted, no path found
    return -1

# Read grid from input and run pathfinding  
input_text = input()
grid = eval(input_text)
result = shortest_safe_path(grid)
print(result)

Now, let’s understand the code step by step:

from collections import deque

def shortest_safe_path(grid):

• We import the deque (double-ended queue) class from the collections module, which provides an efficient way to implement the BFS queue.
• We define the main function shortest_safe_path that takes the grid as input.

# Find exit position
    exit_position = None
    rows = len(grid)
    cols = len(grid[0])
    for i in range(rows):
        for j in range(cols):
            if grid[i][j] == 'E':
                exit_position = (i, j)
                break
        if exit_position:
            break

• We initialize exit_position to None and get the number of rows and columns in the grid.
• We iterate through each cell in the grid using nested loops.
• If we find the exit cell marked as ‘E’, we store its position as a tuple (i, j) in exit_position and break out of both loops.

# If no exit, no path possible
    if not exit_position:
        return -1

• If exit_position is still None after the loop, it means there is no exit cell in the grid.
• In this case, we return -1 to indicate that no path is possible.

# Define possible movement directions
    directions = [(-1, 0), (0, 1), (1, 0), (0, -1)]

• We define a list directions that contains four tuples representing the possible movement directions: up, right, down, and left.
• Each tuple (dr, dc) represents the change in row and column when moving in that direction.

# Initialize BFS
    queue = deque([(0, 0, 0)])  # (row, col, distance)
    visited = set([(0, 0)])  # Track visited cells

• We initialize the BFS queue queue as a deque with a single tuple (0, 0, 0), representing the starting position (0, 0) and a distance of 0.
• We also initialize a set visited to keep track of the cells we have already visited, starting with the initial position (0, 0).

# BFS until queue empty or exit found
    while queue:
        row, col, distance = queue.popleft()
        if (row, col) == exit_position:
            return distance  # Exit found, return path length
        
        # Explore four adjacent cells
        for dr, dc in directions:
            new_row, new_col = row + dr, col + dc
            # Check if new position is valid
            if (0 <= new_row < rows and 
                0 <= new_col < cols and
                (new_row, new_col) not in visited and
                grid[new_row][new_col] != 1):
                queue.append((new_row, new_col, distance + 1))
                visited.add((new_row, new_col))

• We start the BFS loop, which continues until the queue is empty or we find the exit.
• In each iteration, we remove the leftmost element from the queue using queue.popleft(), which represents the current cell we are processing.
• If the current cell matches the exit position, we have found the shortest path, and we return the distance.
• Otherwise, we explore the four adjacent cells by iterating over the directions list.
• For each direction, we calculate the new row and column by adding the corresponding dr and dc values to the current row and column.
• We check if the new position is valid by ensuring it is within the grid boundaries, has not been visited before, and is not a sentinel (value 1).
• If the new position is valid, we append it to the queue along with the updated distance (incremented by 1) and mark it as visited by adding it to the visited set.

# Queue exhausted, no path found
    return -1

• If the BFS loop completes without finding the exit, it means the queue was exhausted, and no path exists.
• In this case, we return -1 to indicate that no safe path was found.

# Read grid from input and run pathfinding  
input_text = input()
grid = eval(input_text)
result = shortest_safe_path(grid)
print(result)

• We read the grid as a string from the user input using input().
• We convert the input string to a 2D list using eval() and store it in the grid variable.
• We call the shortest_safe_path function with the grid as an argument and store the result in the result variable.
• Finally, we print the result, which represents the length of the shortest safe path or -1 if no path exists.

🎉 Triumph in the Skywatch Spire and Beyond! 🏆

Congratulations, brave adventurer! 🌟 Your unwavering determination and sharp programming skills have led you to conquer the treacherous Skywatch Spire and outsmart the rogue Clockwork Sentinels. 💪 The power of Breadth-First Search has illuminated the path to victory, guiding you through the twists and turns of this challenging quest. 🗺️✨

As you stand tall atop the spire, the panoramic view of Eldoria stretches out before you—a testament to the incredible journey you’ve undertaken. 🌄 This CTF has not only tested your technical prowess but also immersed you in a captivating narrative that brought the world of Eldoria to life. 📜🗡️

Through the Clockwork Guardian challenge, you’ve honed your skills in graph traversal, grid-based pathfinding, and efficient algorithm design. 🧩 But more than that, you’ve experienced the thrill of being a hero in a fantastical realm, facing formidable foes and emerging triumphant. 🛡️🐉

As we conclude this epic blog post, I can’t help but feel a sense of accomplishment.

🗺️ Ready for More Adventures?

Want to explore more Cyber Apocalypse 2025 writeups? Check out my other solutions here!