🎼 Enchanted Cipher 🔐
📜 Tales From Eldoria
🗡️ Synopsis
In this cryptography challenge, we must decode messages that have been encrypted using an “enchanted shifting cipher.” 🧙♂️ The cipher operates on groups of 5 alphabetical characters, applying a different random shift to each group. Our task is to reverse the encryption and restore the original plaintext messages. Let’s put our decryption skills to the test! 💪
📜 Description
The Grand Arcane Codex, a repository of historical records, has been corrupted by a mischievous enchantment. 📖✨ Each entry in the codex has been encrypted using a shifting cipher that changes every 5 characters. The encrypted messages are composed of 3-7 randomly generated words. To crack the cipher, we’ll need to analyze the shifting pattern and develop a decryption algorithm. 🔍🔐
The cipher follows these rules:
- Alphabetical characters are processed in groups of 5 (ignoring non-alphabetical characters).
- For each group, a random shift between 1 and 25 is chosen and applied to every letter in that group.
- After the encoded message, an additional line indicates the total number of shift groups.
- The final line lists the random shift values used for each group.
Our quest is to decode the given input and recover the original plaintext message. ⚔️🗝️
🛡️ Skills Required
To conquer this challenge, you’ll need:
- 🔒 Understanding of basic cryptography concepts
- 🔡 Familiarity with the Caesar cipher and letter shifting
- 🐍 Ability to implement decryption algorithms in Python
- 🔍 Careful attention to the cipher’s specific rules and input format
🏆 Skills Learned
By solving this challenge, you’ll gain:
- 🗝️ Experience with decrypting shifted ciphers
- 🎻 Practice parsing and manipulating string input in Python
- 🧩 Improved problem-solving skills for cryptographic challenges
- 🔐 Insight into the workings of multi-shift encryption schemes
⚔️ Solving The Challenge
Let’s break down our Caesar Cipher approach:
🔍 Understanding the Caesar cipher
The Caesar cipher originated in ancient Rome with Julius Caesar himself, who used it for military communications around 58 BCE. As documented by Roman historian Suetonius, Caesar shifted each letter three positions forward in the alphabet to protect sensitive messages from enemies. This simple substitution cipher was revolutionary for its time despite its straightforward mechanism.
The cipher’s historical importance extends beyond Rome. It remained in military use for centuries, with the Russian army still employing variants as late as 1915. In modern cryptography, the Caesar cipher serves as the foundation for more sophisticated encryption methods, including the Vigenère cipher which expanded on its principles by using multiple shift values.
Though easily broken through frequency analysis (a technique pioneered by 9th-century Arab polymath Al-Kindi), the Caesar cipher introduced the fundamental concept of cryptographic keys and established the principle that security could be achieved through mathematical transformations rather than mere secrecy of method.
📥 Understanding the Input
Upon accessing the challenge, we’re presented with a description of the enchanted shifting cipher and an example of its input/output format:
## Example
### Input
ibeqtsl
2
[4, 7]
### Output
exampleLet’s break down this problem in more detail to understand how the cipher works and how we can decipher the encoded message.
In the example provided:
- “ibeqtsl” is the encoded word
- “2” represents the total number of shift groups
- “[4, 7]” specifies the shift values for each group
This type of encryption is known as the Caesar Cipher, named after Julius Caesar who used it to encrypt military messages. Despite its seemingly complicated description, the core concept is quite straightforward to grasp.
The Caesar Cipher works by shifting the alphabet a certain number of positions. Let’s look at a simple example with a shift of 2:
Original: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Shifted: Y Z A B C D E F G H I J K L M N O P Q R S T U V W XNotice how each letter in the original alphabet moves 2 positions forward. ‘A’ becomes ‘C’, ‘B’ becomes ‘D’, and so on. When we reach the end of the alphabet, we wrap around back to the beginning. So ‘Y’ becomes ‘A’, and ‘Z’ becomes ‘B’.
Using this principle, the encrypted word “OtUgxgp” would decrypt to “MrSeven” with a shift of 2.
Now, let’s return to our specific problem. We know “ibeqtsl” should decrypt to “example”, but we need to account for the fact that the cipher uses different shift values for every 5 letters.
To verify our understanding, we can use an online Caesar Cipher tool. Plugging in “ibeqt” and trying a shift of 4 (the first value in our shift array), we get the nonsensical output “mfiux”.
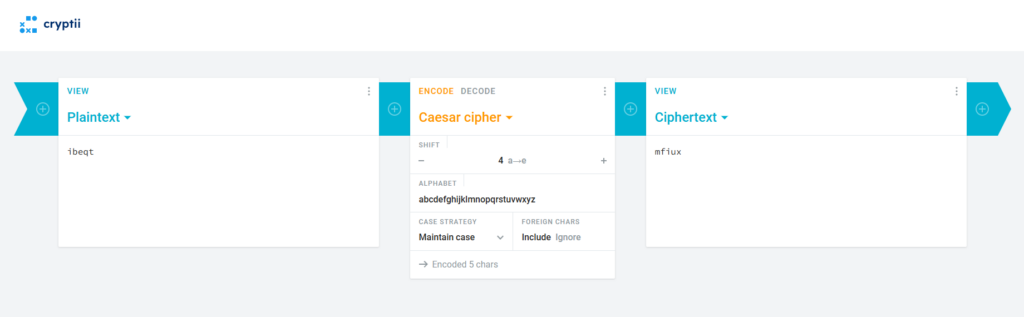
But if we try a shift of -4 instead:
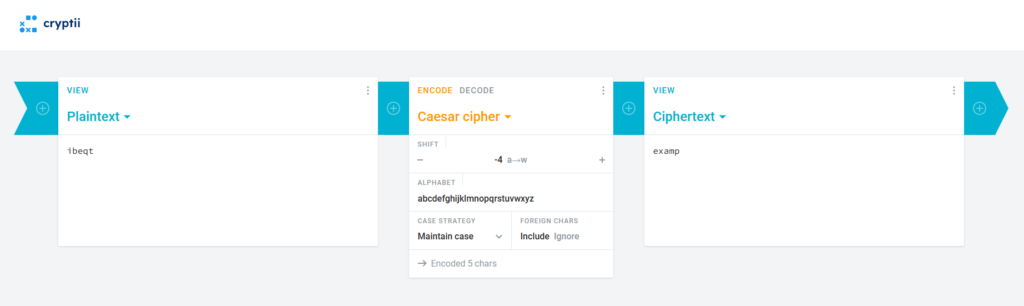
Aha! The first 5 letters, “ibeqt”, decrypt correctly to “examp”. This reveals a key insight – the shift values are applied in the opposite direction. A positive shift in the problem corresponds to shifting backwards in the actual cipher.
To decrypt the remaining 2 letters, “sl”, we use the second shift value of 7:
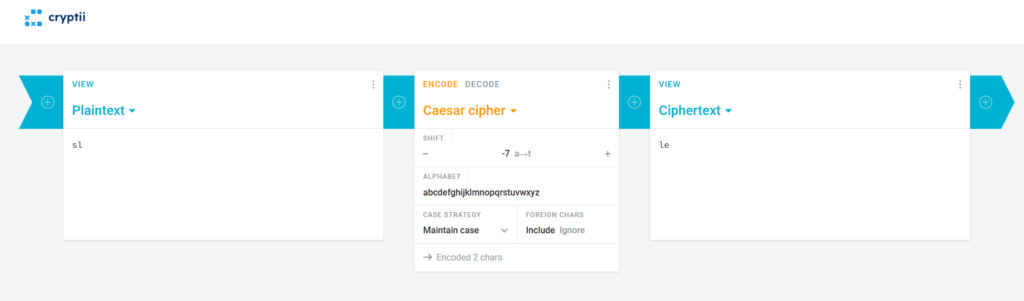
Putting it all together, a shift of -4 gives us “examp”, and a shift of -7 gives us “le”. Combining them yields the original word: “example”. We’ve cracked the code!
The tricky part is implementing this decryption process in code. The first hurdle is figuring out how to handle the input correctly. Initially, it seems input() only returns the encoded text without the number of shifts or shift values. However, after some experimentation, I realized we can call input() multiple times to retrieve each piece of information separately. Let’s take this chance to parse the data into the correct formats as well:
🐍 Implementing the Solution
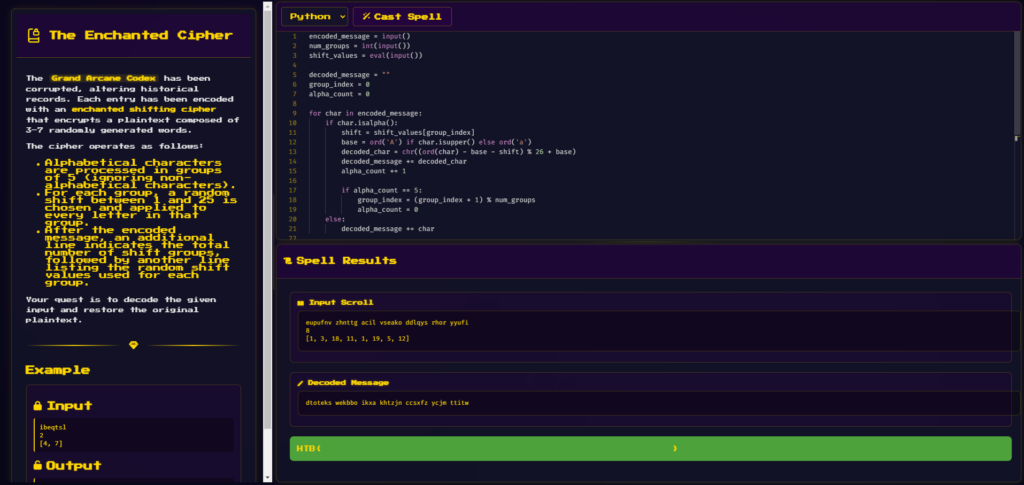
Here’s the complete Python code to solve the Enchanted Cipher challenge:
encoded_message = input()
num_groups = int(input())
shift_values = eval(input())
decoded_message = ""
group_index = 0
alpha_count = 0
for char in encoded_message:
if char.isalpha():
shift = shift_values[group_index]
base = ord('A') if char.isupper() else ord('a')
decoded_char = chr((ord(char) - base - shift) % 26 + base)
decoded_message += decoded_char
alpha_count += 1
if alpha_count == 5:
group_index = (group_index + 1) % num_groups
alpha_count = 0
else:
decoded_message += char
print(decoded_message)
Now, let’s understand the code step by step:
encoded_message = input()
num_groups = int(input())
shift_values = eval(input())
- We read the encoded message, the number of shift groups, and the shift values from the input.
- The encoded message is stored as a string in
encoded_message. - The number of shift groups is converted to an integer using
int()and stored innum_groups. - The shift values are evaluated as a Python expression using
eval(), allowing us to read them as a list of integers.
decoded_message = ""
group_index = 0
alpha_count = 0
- We initialize an empty string
decoded_messageto store the decoded message as we build it. group_indexis set to 0, representing the index of the current shift group being processed.alpha_countis also set to 0, which will keep track of the number of alphabetical characters encountered within each group.
for char in encoded_message:
if char.isalpha():
shift = shift_values[group_index]
base = ord('A') if char.isupper() else ord('a')
decoded_char = chr((ord(char) - base - shift) % 26 + base)
decoded_message += decoded_char
alpha_count += 1
if alpha_count == 5:
group_index = (group_index + 1) % num_groups
alpha_count = 0
else:
decoded_message += char
- We iterate over each character
charin theencoded_message. - If
charis an alphabetical character (checked usingisalpha()), we proceed to decrypt it:- We retrieve the shift value for the current group using
shift_values[group_index]. - We determine the ASCII base value (
'A'for uppercase letters,'a'for lowercase letters) using a ternary operator andord(). After completing the challenge, I don’t think you need to worry about uppercase letters! - We calculate the decoded character by applying the reverse shift using the formula:
(ord(char) - base - shift) % 26 + base.ord(char)converts the character to its ASCII value.- We subtract the base value to normalize the character to a 0-based index.
- We subtract the shift value to reverse the shift operation.
- We take the modulo
% 26to ensure the result stays within the range of the alphabet. - Finally, we add the base value back to obtain the decoded character’s ASCII value.
- The decoded character is then converted back to a character using
chr()and appended todecoded_message. - We increment
alpha_countto keep track of the number of alphabetical characters processed in the current group. - If
alpha_countreaches 5 (indicating we’ve processed a complete group), we updategroup_indexto move to the next group using(group_index + 1) % num_groups. This ensures we wrap around to the first group if we’ve reached the end. - We reset
alpha_countto 0 for the next group.
- We retrieve the shift value for the current group using
- If
charis not an alphabetical character, we simply append it todecoded_messageas is.
print(decoded_message)
- Finally, we print the
decoded_message, which now contains the fully decoded plaintext.
🏆 Triumph over the Enchanted Cipher
Congratulations, brave adventurer! 🎉 Your mastery of cryptography and keen problem-solving skills have allowed you to break the enchantment and restore the corrupted entries of the Grand Arcane Codex. 📜✨
Through your journey, you’ve not only honed your coding abilities but also delved into the fascinating world of ciphers and encryption. Your newfound knowledge of Caesar ciphers and multi-shift schemes will undoubtedly serve you well in future cryptographic challenges. 🗝️💡
But the quest for knowledge and the fight against corruption never ends. As you close the pages of the Grand Arcane Codex, you can’t help but wonder what other mysteries and challenges await you in the vast realm of Eldoria. 🏰🌟
So, keep your skills sharp, your mind open, and your spirit brave. For the power to unravel secrets and restore truth lies within you, noble coder. 💪🧙♂️
🗺️ Ready for More Adventures?
Want to explore more Cyber Apocalypse 2025 writeups? Check out my other solutions here!

