🔮 Summoner Incantation 🧙♂️
📜 Tales From Eldoria
🗡️ Synopsis
Deep within the ancient halls of Eldoria, a powerful secret lies dormant—the Dragon’s Heart. 🐉💗 To awaken its magic, we must harness the energy of delicate incantation tokens. But beware! These tokens are fragile, and combining adjacent ones will cause their energy to dissipate into the void. 💨 Our quest is to determine the maximum amount of energy that can be harnessed by selecting tokens such that no two are adjacent. Let the summoning begin! 🪄
📜 Description
Summoners, heed the call! The Dragon’s Heart 🐉💗 awaits those brave enough to unlock its power. But this is no simple task. The key lies in combining magical incantation tokens in just the right way. 🧩
These tokens are delicate, you see. If you dare to combine two that sit side by side, their energy will be lost forever, scattered to the void. ❌💨 The true path to power is to carefully choose tokens that stand apart, ensuring their energies remain intact. 💪✨
In essence, our challenge is to find the maximum sum achievable by selecting non-adjacent tokens from the list provided. 📝 It’s a test of wit, strategy, and the very laws of magic themselves! 🎩🔮
🛡️ Skills Required
To triumph in this arcane endeavor, you’ll need:
- 🧠 Familiarity with dynamic programming concepts
- 🗺️ Understanding of the “House Robber” problem and its solutions
- 🐍 Ability to implement algorithms in Python
- 🔍 Careful attention to problem constraints and edge cases
🏆 Skills Learned
By summoning the power of the Dragon’s Heart, you’ll gain:
- 💪 Practice applying dynamic programming techniques to optimization problems
- 🌌 Experience efficiently handling input and output in Python
- 🧙♂️ Improved problem-solving skills for tackling complex algorithmic challenges
- 🔮 Insight into the thought process behind solving the “House Robber” problem
⚔️ Solving The Challenge
Let’s break down our House Robber approach:
🔍 Understanding the House Robber
The House Robber algorithm tackles a fascinating optimization problem that elegantly demonstrates dynamic programming principles. Imagine a thief planning to rob houses along a street, with each house containing a specific amount of money. The critical constraint is that the thief cannot rob adjacent houses without triggering an alarm system.
This problem illustrates the powerful concept of optimal substructure – the idea that we can build a solution by solving smaller versions of the same problem. At each house, the thief faces a clear decision: rob this house and skip the next one, or skip this house and preserve the option to rob the next.
The brilliance of the solution lies in its recursive formulation that evolves into an efficient algorithm. For each house, we calculate the maximum possible profit by comparing two options: the value of the current house plus the maximum profit from houses two steps back, or the maximum profit from the previous house (skipping the current one).
What makes this problem particularly instructive is how it transforms a seemingly complex decision tree into a linear calculation through careful state management. The algorithm maintains just two variables that represent the maximum profit possible ending at the previous house and the house before that.
This elegant problem appears frequently in computer science education and technical interviews because it perfectly balances conceptual simplicity with meaningful application of optimization techniques.
📥 Understanding the Input
Upon accessing the challenge, we’re presented with a description and how the input works
- Input: A single line containing a Python-style list of integers (token energies)
- Output: A single integer representing the maximum energy obtainable
Ah, but this is no ordinary challenge, you see. It’s a tale as old as time, a problem known far and wide as the “House Robber.” 🏚️💰 But fear not, for with a little bit of magic (and some dynamic programming), we shall prevail! 💪✨
🐍 Implementing the Solution
Here’s the complete Python code to solve the Summoner Incantation challenge:
input_text = input()
nums = eval(input_text)
def max_sum_non_adjacent(nums):
include = nums[0]
exclude = 0
for i in range(1, len(nums)):
new_include = exclude + nums[i]
exclude = max(include, exclude)
include = new_include
return max(include, exclude)
print(max_sum_non_adjacent(nums))
Let’s analyze this elegant and very simple solution to the Summoner Incantation challenge:
input_text = input()
nums = eval(input_text)
These lines handle reading the input. The code takes a string representation of a list and converts it to an actual Python list using eval(). This gives us our array of “house values” that we’ll work with.
def max_sum_non_adjacent(nums):
include = nums[0]
exclude = 0
for i in range(1, len(nums)):
new_include = exclude + nums[i]
exclude = max(include, exclude)
include = new_include
return max(include, exclude)
This function implements dynamic programming with constant space complexity. Let me break down what’s happening:
include = nums[0]
exclude = 0
We initialize two variables that represent our two possible states:
include: The maximum sum if we include the current elementexclude: The maximum sum if we exclude the current element
We start by assuming we’ll include the first element.
for i in range(1, len(nums)):
new_include = exclude + nums[i]
exclude = max(include, exclude)
include = new_include
For each element (starting from the second one):
- We calculate a new “include” value by adding the current element to the previous “exclude” sum
- We update “exclude” to be the maximum of the previous “include” or “exclude”
- We update “include” with our newly calculated value
This clever approach maintains only the information we need about the previous elements without storing the entire solution history.
return max(include, exclude)
Finally, we return the maximum of our two possibilities, which represents the maximum possible sum we can achieve.
print(max_sum_non_adjacent(nums))
We call our function with the input array and print the result.
By carefully considering each token and updating our “include” and “exclude” energies, we arrive at the optimal incantation. The power of the Dragon’s Heart is ours to wield! 🐉💗
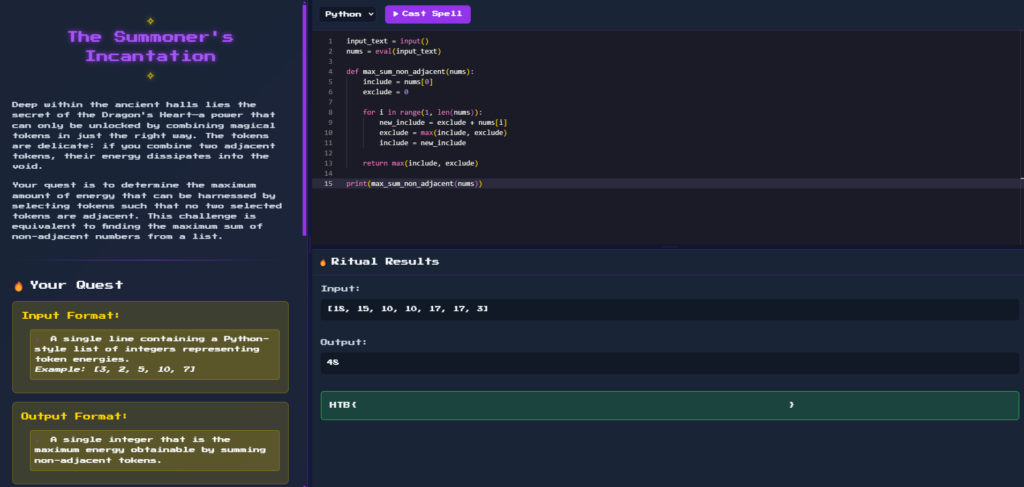
🏆 Triumph in the Ancient Halls
Congratulations, brave summoner! 🎉 Your mastery of the arcane arts and keen problem-solving skills have unlocked the secret of the Dragon’s Heart. 🐉💗 The ancient halls echo with the thunder of your triumph! ⚡🎉
Through this challenge, you’ve not only honed your programming prowess but also delved into the mystical world of dynamic programming. The techniques you’ve learned here will serve you well in future algorithmic quests. 🗺️💪
But remember, the path of a true summoner is never-ending. There are always new spells to learn, new problems to conquer, and new realms of knowledge to explore. 📚✨
So keep your skills sharp, your mind open, and your heart brave. The universe of coding challenges awaits, and with the power of the Dragon’s Heart at your command, no problem shall stand in your way! 🌟💪
🗺️ Ready for More Adventures?
Want to explore more Cyber Apocalypse 2025 writeups? Check out my other solutions here!
